Imagine gazing upon a small, seemingly insignificant clay tablet from ancient Babylon, its surface covered in wedge-shaped cuneiform inscriptions. At first glance, it appears to be just another relic from a civilization long gone. Yet hidden within its humble frame lies one of the most astonishing mathematical discoveries of the ancient world. This artifact, known today as Plimpton 322, has fascinated historians, mathematicians, and archaeologists for decades, challenging our understanding of the history of mathematics and offering profound insights into a civilization that thrived thousands of years ago.
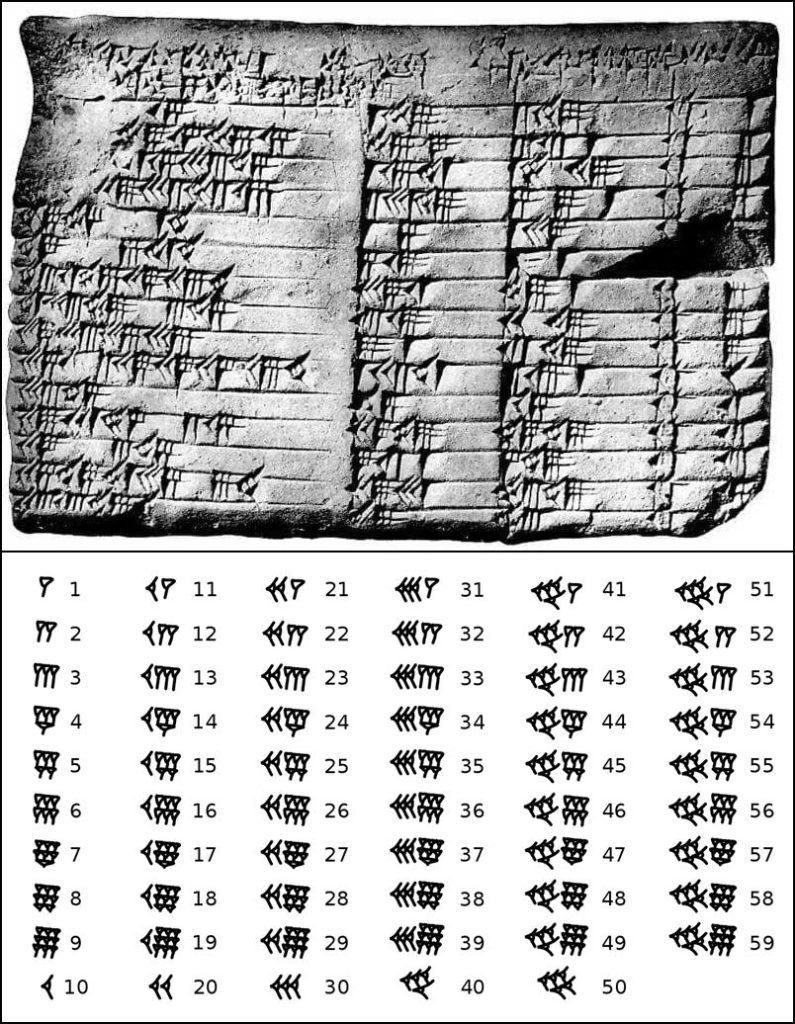
For many years, scholars believed that Plimpton 322 contained a simple list of Pythagorean triples—sets of three numbers that satisfy the famous equation a² + b² = c². These triples, used today in understanding right-angled triangles, are fundamental in modern mathematics. However, a groundbreaking new interpretation has emerged in recent years, reshaping how we view this remarkable artifact. Researchers now argue that Plimpton 322 may be far more than a list of numerical patterns—it could very well be the world’s oldest trigonometric table. If this interpretation holds true, it would mean that the Babylonians were exploring trigonometric relationships nearly a thousand years before the ancient Greek astronomer Hipparchus, long considered the father of trigonometry, ever put pen to papyrus.
What makes this possibility so extraordinary is the method the Babylonians may have used. Unlike our current decimal system, which is based on the number 10, the Babylonians used a base 60 system—an approach that might seem foreign to us today but is actually still reflected in how we tell time, divide circles into degrees, or measure angles. Using this base 60 system, the Babylonians developed a highly accurate and innovative way of calculating trigonometric values. Some modern researchers suggest that in certain respects, their method may even surpass the trigonometric techniques we use today, especially in terms of precision and simplicity when dealing with rational numbers.
Daniel Mansfield, a mathematician and key figure in this research, emphasizes the importance of reexamining ancient mathematical texts with fresh eyes. “There is a vast collection of Babylonian tablets,” he explains, “but we’ve only just scratched the surface. We’re beginning to realize that this ancient culture had an incredibly advanced understanding of mathematics that we are only now starting to appreciate.” According to Mansfield, Plimpton 322 is not just a relic; it’s a window into the minds of scholars from a civilization that was far ahead of its time in many intellectual disciplines.
However, as with many revolutionary ideas, this new interpretation has not gone unchallenged. The claim that Plimpton 322 represents a form of trigonometry has sparked debate across the academic world. Some critics argue that the tablet has been mischaracterized, suggesting instead that it may have served as a teaching tool or a classroom aid for scribes learning mathematical principles. Others contend that the current interpretation is being used to support broader theories, such as “rational trigonometry,” a concept that deviates from traditional views of angle-based calculations. These critics maintain that while the tablet is indeed mathematically significant, it may not represent trigonometry as we understand it today.
Despite these disagreements, the attention surrounding Plimpton 322 has had a positive effect: it has reignited global interest in ancient mathematics and the intellectual contributions of non-Western civilizations. Researchers are now reexamining Babylonian tablets with renewed focus, searching for additional clues that might support or refute the trigonometric interpretation. This renewed curiosity is not limited to academia—educators, museum curators, and even casual history enthusiasts have joined the conversation, eager to explore the depths of Babylonian knowledge and understand its relevance to modern thought.
The study of Plimpton 322 serves as a powerful reminder that the roots of science and mathematics extend far beyond the boundaries of classical Greece and Rome. The Babylonians, often overshadowed in popular history by their Egyptian and Greek counterparts, were cultivating a rich and nuanced intellectual tradition of their own. Their use of the sexagesimal system, their astronomical records, and their contributions to algebraic thinking all point to a society that deeply valued knowledge, precision, and education. Plimpton 322 offers compelling evidence that they also had a grasp of geometric relationships that could qualify as an early form of trigonometry.
As we continue to investigate this mysterious clay tablet, we are drawn into a broader reflection on human ingenuity. How many more secrets are buried beneath the sands of Mesopotamia? How much of our shared intellectual heritage remains undiscovered, hidden in dusty storerooms, waiting for a curious mind to unlock its potential? Each discovery, like that of Plimpton 322, brings us closer to a fuller picture of our ancestors’ capabilities and invites us to reimagine the history of science and mathematics through a more inclusive and global lens.
Ultimately, Plimpton 322 is far more than a piece of clay from an ancient city. It is a symbol of curiosity, resilience, and the enduring human drive to understand the world. Whether it proves to be the oldest trigonometric table or simply an ingenious pedagogical tool, it has already achieved something remarkable—it has forced us to question long-held assumptions, to look beyond the familiar narratives, and to acknowledge that genius can emerge in any time, from any culture, in any corner of the world. As scholars continue to debate its meaning and significance, Plimpton 322 reminds us that the past is never truly settled—it is alive, waiting to be discovered anew.





